Interested to collaborate? Let’s get in touch!
Exact
After having been the lead developer of RoundingSat in the years 2019-2020, the time has come to continue this work in my own fork.
The Exact solver streamlines the different techniques present in RoundingSat, and adds some interesting features such as support for .mps and .lp files and a novel at-most-one cardinality detection algorithm.
Feel free to try it out, it should be one of the most effective general binary linear programming solvers on the planet! 😉
I’m planning to post some plots showcasing Exact’s performance soon, but for now, I’ll leave the RoundingSat ones up below.
RoundingSat
RoundingSat is a novel combinatorial solver taking 0-1 integer linear constraints as input. It outputs a solution if it exists or a certificate of unsatisfiability otherwise. In the optimization case, the solution is optimal with as witness an outputted certificate of optimality.
RoundingSat’s unique selling point is its construction of cutting planes proofs during search. Cutting planes proofs are related to MIP cut generation, but instead of deriving cutting planes from a rational solution to the relaxed problem, a cutting plane is derived from a failing search branch. By quickly traversing depth-first search branches, RoundingSat accumulates a database of derived cutting planes, eventually leading to a solution or a proof that no (better) solution exists.
In effect, RoundingSat constructs a cutting planes proof, generalizing the resolution proof constructed by modern SAT solvers. RoundingSat, hence, does not suffer the lower-bound exponential running times exhibited by resolution-based systems on many important problems.
Compared to branch-and-cut systems, RoundingSat retains excellent performance on problems where the linear relaxation does not provide much guidance to the optimal solution. As a bonus, RoundingSat provides machine-verifiable certificates of unsatisfiability and optimality upon request, which are useful for verification purposes or as rigorous mathematical proofs.
One year of progress
Below CDF plots give an indication of RoundingSat’s potential, as well as its performance improvement year by year. At this rate, RoundingSat will soon rival and hopefully surpass commercial MIP solvers on even the MIPLIB benchmark set. It is worth noting that at the moment, RoundingSat employs no preprocessing whatsoever; it relies mainly on deriving as many cutting planes as possible.
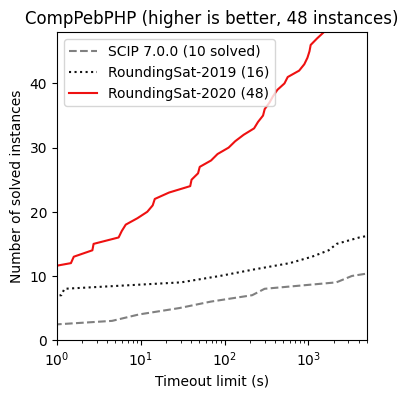
Proof-complexity inspired problem designed to be hard for MIP solvers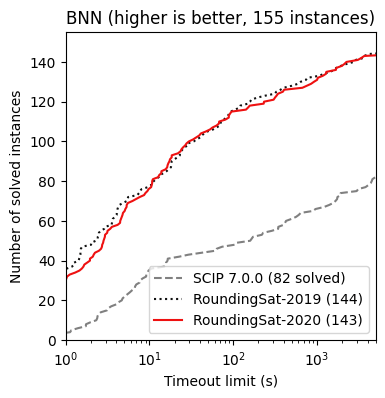, courtesy of Jakob Nordström 
Binarized neural network transition models 
Stable matching with ties and incomplete lists, courtesy of William Pettersson 
Pseudo-Boolean competition 2016, small-coefficient optimization track 
MIPLIB 0-1 integer instances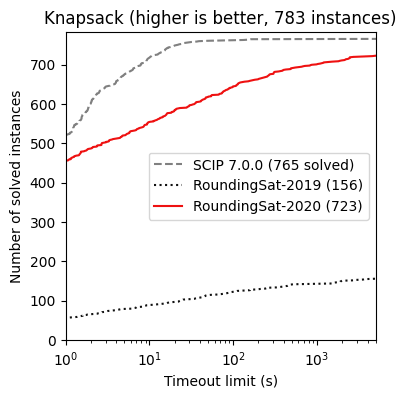 
Hard knapsack instances. Note that the MIP solver SCIP uses specialized dynamic programming to solve these instances, while RoundingSat simply uses its general cutting planes routine.
jodevriendt.com 